Урок математики (По древним майя)

Урок математики

Дешифровка цифровых знаков майя не составила большого труда для ученых. Причиной тому - порази­тельная простота и доведенная до. совершенства ло­гичность системы их счета. Можно лишь без конца изумляться великой мудрости народа, сумевшего практически в одиночку подняться на недоступные вершины абстрактного математического мышления, одновременно приспособив его к своим конкретно-практическим земным нуждам. Чванливая Европа еще считала по пальцам, когда математики древних майя ввели понятие нуля и оперировали бесконечно боль­шими величинами. Разве это не удивительно?..

Древние майя пользовались двадцатеричной си­стемой счисления, или счета. Почему именно число 20 наряду с единицей стало основой их счета, сейчас невозможно установить с достаточной достовер­ностью. Но на помощь приходит простая логика. Она подсказывает, что скорее всего сам человек был для древних майя той идеальной математической мо­делью, которую они и взяли за единицу счета. Дейст­вительно, что может быть естественней и проще, коль скоро сама природа «расчленила» эту единицу «сче­та» на 20 единиц второго порядка по числу пальцев на руках и ногах. Тут и выдумывать ничего не нужно, ибо ты сам являешь собою превосходную и к тому же уже решенную арифметическую задачу!

Между прочим, подтверждение именно такому объяснению возникновения двадцатеричной системы счета мы находим в этимологической связи слова «виналь» - так на языке майя назывался двадца­тидневный месяц - со словами «двадцать» и «че­ловек». По-видимому, говоря «один человек», древ­ние майя механически представляли себе число «20», если, конечно, в это время речь шла о каких-то ко­личественных единицах.

Известно, что европейцы, как, впрочем, и подав­ляющее большинство народов мира, пользуются сей­час так называемой арабской цифровой системой, со­зданной в Индии лишь в конце первой половины про­шлого тысячелетия (V век). В соответствии с этой си­стемой- ради справедливости ее следовало бы назы­вать индийской - мы расставляем цифровые зна­ки горизонтально - строчечным способом, применяя «позиционный принцип» - одно из замечательных достижений человеческого разума. Это значит, что цифры стоят друг за другом в строгом порядке, справа налево от первой позиции или первого поряд­ка к последующим, а именно: единицы, десятки, сот­ни, тысячи и т. д.

Древние майя также пришли к использованию по­зиционного принципа. В отличие от нас, европейцев, им не у кого было заимствовать это принцип, и тог­да они сами додумались до него, причем почти на целое тысячелетие (!) раньше Старого Света. Однако запись цифровых знаков, образующих число, они ста­ли вести не горизонтально, а вертикально, снизу вверх, как бы возводя некую этажерку из цифр. Поскольку счет был двадцатеричным, то каждое начальное чис­ло следующей верхней позиции, или порядка, было в двадцать раз больше своего соседа с нижней полки «этажерки майя» (если бы майя пользовались десяте­ричной системой, то число было бы больше не в два­дцать, а только в десять раз). На первой полке стоя­ли единицы, на второй - двадцатки и т. д.

Майя записывали свои цифровые знаки в виде то­чек и тире, причем точка всегда означала единицы данного порядка, а тире - пятерки (Особый знак для пятерки послужил основанием для зачисления системы счета древних майя в так называемую пятерично-двадцатеричную, однако вряд ли можно согласиться с этим, поскольку пятерки-тире лишь упрощали написание цифровых знаков, не внося каких-либо принципиальных изменений в двадцатеричную систему счета.). Цифровые зна­ки древних майя смотрите на 72-й странице.

В приведенной таблице не хватает двадцатой цифры. Но это не 20, ибо у майя 20, так же *$ак у нас 10, было уже не цифрой, а составным двузнач­ным числом. Двадцатой цифрой счета древних майя был «нуль», и изображался он в виде стилизованной раковины:

Цифра 'нуль'

В двадцатеричной системе, знающей понятие нуля, первым двузначным числом могло быть только число 20. Так оно и было. Но как изобразить его? И майя решают эту задачу необычайно просто: над ракови­ной-нулем они рисуют точку, то есть первую циф­ру своего счета. Новый знак - он изображался так:

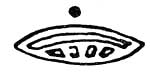
Первоначальная единица счета второй позиции многозначного числа

- обозначал первоначальную единицу сче­та второй позиции или второй полки многозначного числа (многополочной этажерки).

Система чисел майя

Однако на этом похождения раковины-нуля не кончались. Раковина все же стала появляться и без точки, располагаясь на разных полках цифровой эта­жерки майя. Это означало, что настоящее число бы­ло образовано без участия единиц той полки, на ко­торой в данном случае находилась раковина. Она го­ворила, что единиц этой полки (на которой она рас­положилась) попросту нет, как нет, например, десят­ков, сотен или тысяч в числе, записанном арабскими цифрами, если на отведенном для них месте стоят нули.

Но коль скоро в числе наличествовала хотя бы одна-единственная единица любой из полок, довольно сложный рисунок раковины-нуля сразу же исчезал с нее. Покажем это условно на простейшем примере: + 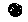= 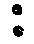, что соответствует числу 21 в нашем представлении.

Действительно, если нижняя точка находится на нижней полке, то это обозначает наличие одной еди­ницы первой позиции, или, попросту говоря, «едини­цу», но уже не как абстрактный цифровой знак, а как конкретное число. Верхняя же полка указывает на наличие одной единицы второго порядка, каковой является двадцатка в двадцатеричной системе. Сле­довательно, перед нами двузначное число 21, образо­ванное в полном соответствии со строгими законами позиционного принципа, но только расположенное не горизонтально, как мы привыкли, а вертикально. Про­верим свой вывод простейшим арифметическим дей­ствием - сложением:

1 «единица» + 1 «двадцатка» = 21.

Чтобы окончательно усвоить урок математики майя, рассмотрим написание нескольких двузначных чисел майя; они наглядно продемонстрируют технику применения ими позиционного принципа, условно на­званного нами «числовой этажеркой майя»:

Числовая этажерка майя

Здесь было бы вполне естественно написать «и так далее», однако это самое «и так далее» как раз и не получается...

В двадцатеричной системе счета древних майя есть исключение: стоит прибавить к числу «359» только одну-единственную единицу первого порядка, как это исключение немедленно вступает в силу. Суть его сводится к следующему: число 360 является началь­ным числом третьего порядка (!), и его место уже не на второй, а на третьей полке.

Но тогда выходит, что начальное число третьего по­рядка больше начального числа второго не в два­дцать раз (20 X 20 = 400, а не 360!), а только в восем­надцать! Значит принцип двадцатеричности нарушен! Все верно. Дело обстоит именно так. Это и есть исключение.

Но чем оно вызвано? - естественно возникает во­прос. А вызвано оно - что самое удивительное - соображениями сугубо практического характера, и можно лишь в который раз изумляться и восхищаться поразительной мудрости, невероятному рационализму этого народа, создателя великой цивилизации.

Оказывается, майя не побоялись нарушить строгий, четкий строй двадцатеричной системы, чтобы приспо­собить абстрактное построение чисел к своим кон­кретным нуждам. И сделали это столь же просто, сколь гениально. Математические расчеты с примене­нием многозначных чисел у майя были в основном связаны с астрономическими вычислениями, которые лежали в основе календаря. Чтобы упростить их, они максимально приблизили первоначальное число треть­его порядка к числу... дней своего года. Ведь в восем­надцати двадцатидневных месяцах, составляющих ка­лендарный год майя, число дней как раз и будет рав­но 360!

Так, начав с конкретного (один человек - два­дцать пальцев), древние майя поднялись на вершину абстрактного мышления, создав двадцатеричную си­стему счета. Однако, обнаружив известные неудобства в абстрактном, они решительно приспособили его к своим практическим нуждам!

При образовании чисел четвертой и всех последую­щих полок-позиций «этажерки майя» принцип двадца-теричности вновь восстанавливается: первоначальное число четвертого порядка - 7200 (360 X 20); пято­го - 144 000 (7200 X 20) и так до бесконечно боль­ших величин. Интересно отметить, что майя были зна­комы с ними не только теоретически. Вспомним хотя бы стелу из священного города Копана, на которой жрецы записали начальную, правда мифическую, да­ту летосчисления майя - 5 041 738 год до нашей эры!